Polynomial trend equation and forecast

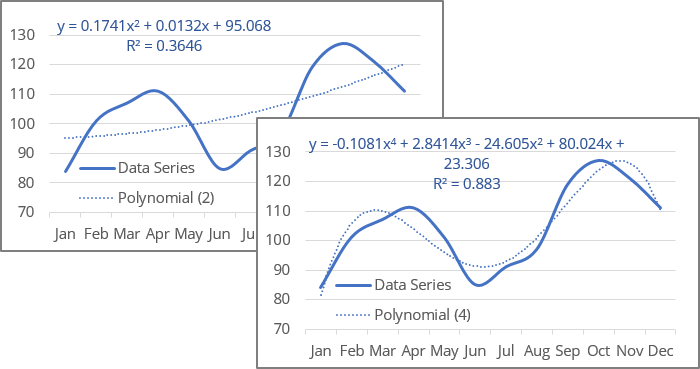
The charts above show polynomial trendlines for the same data with a degree of 2 - the minimum degree of a polynomial trendline in Excel - and 4.

The degree of the polynomial determines the maximum number of extrema - local minima or maxima of the curve:

• A polynomial trendline of the second degree (also known as a Quadratic polynomial trend line) can describe only one maximum or minimum (one hill or valley).
• A polynomial trendline of the third degree (also known as a Cubic polynomial trend line) has one or two extrema.

The maximum degree of the polynomial trendline that can be displayed in an Excel chart is 6:

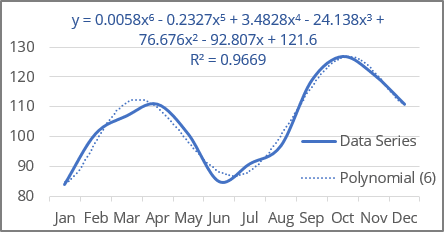
The degree of the polynomial is specified in the Order field - see more about the polynomial trendline in Excel.

Excel uses the least squares method to fit a polyline for the data points.

For a trend line, two sets of variables are required:

• an independent, predictor, or explanatory variable x (named as known_x's),
• a dependent or response variable y (named as known_y's).

Polynomial trendline equation and formulas

The polynomial trendline is a curved line with the function:

   y = a_n*xⁿ + ... +  a₃*x³ + a₂*x² + a₁*x + b

where:

• a_n, ..., a₃, a₂, a₁ and b are calculated parameters of the function (also named function coefficients or constants) that describe the relationship between x and y,
• n is the degree of the polynomial (in Excel, the order of a polynomial). Excel works with polynomial orders from 2^nd to 6^th.

Note: Excel uses a linear model: the polynomial function y = a_n*xⁿ + ... +  a₃*x³ + a₂*x² + a₁*x + b is transformed to a linear function using a change of variables. After changing the variables to X_i = xⁱ, the calculations are completely similar to the linear case y = a_n*X_n + ... + a₃*X₃ + a₂*X₂ + a₁*x + b. Now the variable y does not depend on one variable x in n different degrees but on n independent variables X_i.

Excel offers the following functions to calculate the trend parameters:

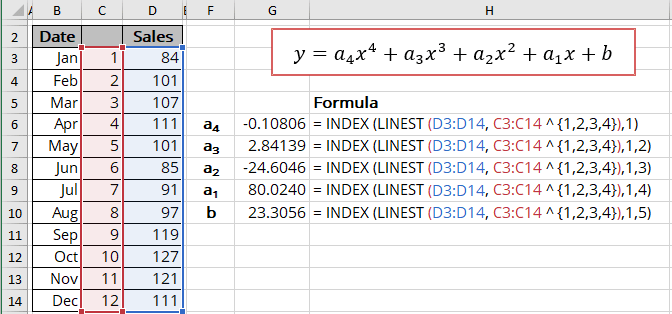
The 4^th order or 4^th degree polynomial trendline

• Equation: y = a₄*x⁴ +  a₃*x³ + a₂*x² + a₁*x + b
• a₄: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4}), 1)
• a₃: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4}), 1, 2)
• a₂: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4}), 1, 3)
• a₁: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4}), 1, 4)
• b: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4}), 1, 5)

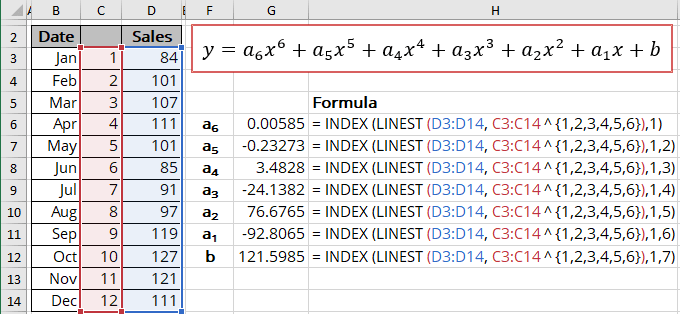
The 6^th order or 6^th degree polynomial trendline

• Equation: y = a₆*x⁶ + a₅*x⁵ + a₄*x⁴ +  a₃*x³ + a₂*x² + a₁*x + b
• a₆: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1)
• a₅: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 2)
• a₄: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 3)
• a₃: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 4)
• a₂: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 5)
• a₁: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 6)
• b: = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,4,5,6}), 1, 7)

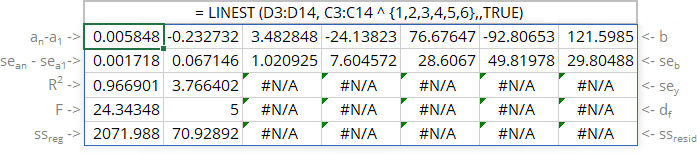
The array function LINEST () calculates the linear trend that fits best the known data and then returns an array with statistics describing the trend line:

= LINEST (known_y's, [known_x's], [const], [stats])

where:

• known_y's (required) are dependent data values,
• known_x's (optional) are independent data values:

  These variables cannot be omitted for the correct calculation for a polynomic trend. In any case, you should provide the known_x's or the array {1,2,3,...} that is the same size as known_y's,

• const (optional) is a Boolean value specifying whether to force the parameter b (intercept) to equal 0:
  • If const is TRUE or omitted, the parameter b is calculated normally,
  • If const is FALSE, the parameter b is set equal to 0.
• stats (optional) is a Boolean value specifying whether to return additional regression statistics:
  • If stats is TRUE, the LINEST () function returns the additional regression statistics in the form of an array:
    

    where:

    Line	Statistics			Description
    1	an	*** a1	b	Parameters of the function
    2	sean	*** sea1	seb	Standard error of each parameter
    3	R2			R-squared value
    		sey		Standard error of y estimate (also known as Standard Error of a regression) shows how big the prediction error is
    4	F			F statistic (F-observed value)
    		dr		Degrees of freedom
    5	ssreg			Regression sum of squares (also known as SSR)
    		ssresid		Residual sum of squares (also known as SSE)

  • If stats is FALSE or omitted, the function returns only the calculated parameters.

For the 6^th degree polynomial trend:

Notes:

1. If you have a version of Microsoft Excel other than Microsoft 365, functions that return arrays must be entered as array functions using Ctrl+Shift+Enter unless you can just press Enter.
2. Because the LINEST () function returns an array of data, you can use the INDEX () function to display only the desired parameter(s) from the returned data array.

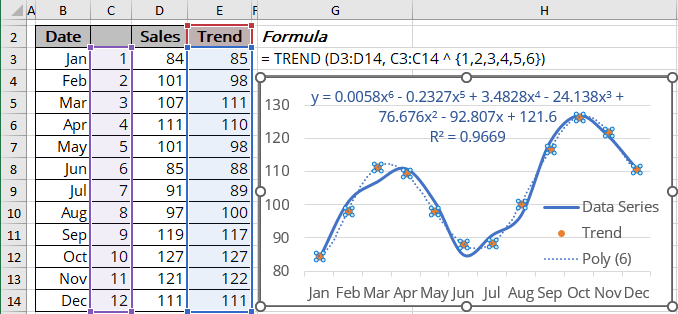
Calculating the polynomial trendline values

To calculate the polynomial trendline values, Excel offers the array function TREND () (see the notes above about array functions) that returns values along a linear trend. To work with this function for polynomial trends, just use the indicated powers of the known_x's instead of known_x's:

= TREND (known_y's, [known_x's], [new_x's], [const])

where:

• known_y's (required) are dependent data values,
• known_x's (optional) are independent data values:

  These values cannot be omitted for the correct calculation for a polynomial trend. In any case, you should provide the known_x's or the array {1,2,3,...} that is the same size as known_y's,

• new_x's (optional) are the new x-values for which the TREND () function should calculate corresponding y-values:
  • If you omit new_x's, it is assumed to be the same as known_x's,
• const (optional) is a Boolean value specifying whether to force the parameter b to 0:
  • If const is TRUE or omitted, the parameter b is calculated normally,
  • If const is FALSE, the parameter b is set to 0.

R-squared value

The R-squared value (in Excel, R²) calculates how well a trendline fits the data. The R-squared value can vary from 0 to 1: the nearer R² is to 1, the better the trendline fits the data.

The R-squared value can be displayed on the chart (see how to turn on the R-squared value). You can easily calculate that value using one of the methods:

• Use the LINEST () function to return the first statistics of the third line of the statistics array:

  = INDEX (LINEST (known_y's, known_x's ^ {1,2,3,...}, , TRUE), 3, 1):

  
• Use the RSQ () function that returns the R-squared value of two data sets:

  = RSQ (array1, array2)

  where array1 and array2 (both are required) are two data sets: